Answer:
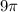 , which is approximately
, which is approximately
 .
.
Explanation:
Consider two sectors in the same circle. The area of the two sectors is proportional to their central angles. In other words, if the central angle is
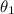 for the first sector in this circle, and
for the first sector in this circle, and
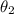 for the second, then:
for the second, then:
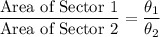 .
.
In this question, think about the whole circle as a sector. The central angle of this "sector" would be
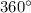 (a full circle.) Compare the area of this circle to that of the
(a full circle.) Compare the area of this circle to that of the
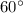 -sector in this circle:
-sector in this circle:
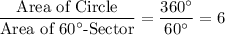 .
.
In other words, the area of this circle is six times that of the
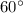 -sector in it.
-sector in it.
The area of that
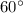 -sector is
-sector is
 . Therefore, the area of this full circle will be
. Therefore, the area of this full circle will be
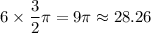 .
.