Question

A lawn sprinkler located at the corner of a yard is set to rotate 50 degrees and project water out 30.0 feet. To the nearest tenth of a foot, what area of the lawn is watered by the sprinkler

Answer 1

Area of the lawn is watered by the sprinkler is 392.75 ft²

Explanation:

As the lawn sprinkler rotate 50 degrees when it project water out, it makes an arc from the corner where it is located.

The area of the lawn in which the water sprinkles, forms a sector with an angle of 50 degrees and radius of 30.0 feet.

`Area \ of \ sector = Area \ of \ lawn= (\theta)/(360) \pi r^2\\\\ Area \ of \ lawn= (50)/(360) \pi (30)^2 = 392.75 \ ft^2`

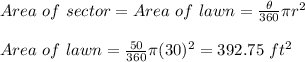
Therefore, area of the lawn is watered by the sprinkler is 392.75 ft²