Question

1. If 5tanA=4, Find the value of (5sinA-3cosA)/(4cosA+5sinA)

2. Solve for θ, sinθ/(1+cosθ) + (1+cosθ)/sinθ =4, 0°<θ<90°
3. Prove that tan⁡〖θ-cot⁡θ 〗 = (〖2sin〗^2 θ-1)/sinθcosθ
4. Without using trigonometric tables ,show that
tan 10°tan15°tan75°tan80°=1
5. If x=acosθ-bsinθ and y=asinθ + bcosθ prove that x^2+y^2=a^2+b^2

Answer 1

1. (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) = 1/8

2. θ = 30°

3. tan(θ) - cot(θ) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))

from tan(θ) - 1/tan(θ) = sin(θ)/cos(θ) - cos(θ)/sin(θ) and sin²(θ) + cos²(θ) = 1

4. tan10°·tan15°·tan75°·tan80°= 1 from;

sin(α)·sin(β) = 1/2[cos(α - β) - cos(α + β)]

cos(α)·cos(β) = 1/2[cos(α - β) + cos(α + β)]

5. x² + y² = a² + b² where x = a·cosθ - b·sinθ and y = a·sinθ + b·cosθ from;

cos²θ + sin²θ = 1

Explanation:

1. Here we have 5·tan(A) = 5·sin(A)/cos(A) = 4

∴ 5·sin(A) = 4·cos(A)

Hence to find the value of (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) we have;

Substituting the value for 5·sin(A) = 4·cos(A) into the above equation in both the numerator and denominator we have;

(4·cos(A) - 3·cos(A)/(4·cos(A) + 4·cos(A)) = cos(A)/(8·cos(A)) = 1/8

Therefore, (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) = 1/8

2. For the equation as follows, we have

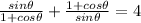`(sin \theta)/(1 + cos \theta) + (1 + cos \theta)/(sin \theta) = 4` this gives

`(2sin (\theta/2) cos (\theta/2) )/(2 cos^2 (\theta/2)) + (2 cos^2 (\theta/2))/(2sin (\theta/2) cos (\theta/2) ) = 4`

`tan(\theta)/(2) + (1)/(tan(\theta)/(2) ) = 4`

`tan^2(\theta)/(2) + 1 = 4* tan(\theta)/(2)`

`tan^2(\theta)/(2) - 4\cdot tan(\theta)/(2) + 1 = 0`

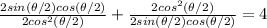
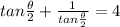
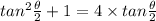
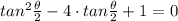
We place;

`tan(\theta)/(2) = x`

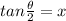
∴ x² - 4·x + 1 = 0

Factorizing we have

(x - (2 - √3))·(x - (2 + √3))

Therefore, tan(θ/2) = (2 - √3) or (2 + √3)

Solving, we have;

θ/2 = tan⁻¹(2 - √3) or tan⁻¹(2 + √3)

Which gives, θ/2 = 15° or 75°

Hence, θ = 30° or 150°

Since 0° < θ < 90°, therefore, θ = 30°

3. We have tan(θ) - cot(θ) = tan(θ) - 1/tan(θ)

Hence, tan(θ) - 1/tan(θ) = sin(θ)/cos(θ) - cos(θ)/sin(θ)

∴ tan(θ) - 1/tan(θ) = (sin²(θ) - cos²(θ))/(cos(θ)×sin(θ))...........(1)

From sin²(θ) + cos²(θ) = 1, we have;

cos²(θ) = 1 - sin²(θ), substituting the value of sin²(θ) in the equation (1) above, we have;

(sin²(θ) - (1 - sin²(θ)))/(cos(θ)×sin(θ)) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))

Therefore;

tan(θ) - cot(θ) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))

4. tan10°·tan15°·tan75°·tan80°= 1

Here we have since;

sin(α)·sin(β) = 1/2[cos(α - β) - cos(α + β)]

cos(α)·cos(β) = 1/2[cos(α - β) + cos(α + β)]

Then;

tan 10°·tan15°·tan75°·tan80° = tan 10°·tan80°·tan15°·tan75°

tan 10°·tan80°·tan15°·tan75° =
`(sin(10^(\circ)))/(cos(10^(\circ))) * (sin(80^(\circ)))/(cos(80^(\circ))) * (sin(15^(\circ)))/(cos(15^(\circ))) * (sin(75^(\circ)))/(cos(75^(\circ)))`

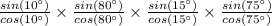
Which gives;

`(sin(10^(\circ)) \cdot sin(80^(\circ)))/(cos(10^(\circ))\cdot cos(80^(\circ))) * (sin(15^(\circ)) \cdot sin(75^(\circ)))/(cos(15^(\circ))\cdot cos(75^(\circ)))`

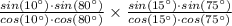
`=(1/2[cos(80 - 10) - cos(80 + 10)])/(1/2[cos(80 - 10) + cos(80 + 10)]) * (1/2[cos(75 - 15) - cos(75 + 15)])/(1/2[cos(75 - 15) + cos(75 + 15)])`

`=(1/2[cos(70) - cos(90)])/(1/2[cos(70) + cos(90)]) * (1/2[cos(60) - cos(90)])/(1/2[cos(60) + cos(90)])`

`=([cos(70)])/([cos(70) ]) * ([cos(60)])/([cos(60) ]) =1`

5. If x = a·cosθ - b·sinθ and y = a·sinθ + b·cosθ

∴ x² + y² = (a·cosθ - b·sinθ)² + (a·sinθ + b·cosθ)²

= a²·cos²θ - 2·a·cosθ·b·sinθ +b²·sin²θ + a²·sin²θ + 2·a·sinθ·b·cosθ + b²·cos²θ

= a²·cos²θ + b²·sin²θ + a²·sin²θ + b²·cos²θ

= a²·cos²θ + b²·cos²θ + b²·sin²θ + a²·sin²θ

= (a² + b²)·cos²θ + (a² + b²)·sin²θ

= (a² + b²)·(cos²θ + sin²θ) since cos²θ + sin²θ = 1, we have

= (a² + b²)×1 = a² + b²