Question

2. Inflation is at a rate of 7% per year. Evan's favorite bread now costs $1.79. What did it cost 10 years ago? How long

before the cost of the bread doubles?​

Answer 1

It cost $0.91 10 years ago.

It takes 10.24 years for the cost of bread to double.

Explanation:

The equation for the price of bread after t years has the following format:

`P(t) = P(0)(1+r)^(t)`

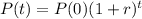
In which P(0) is the current price, and r is the inflation rate, as a decimal.

If we want to find the price for example, 10 years ago, we find P(-10).

Inflation is at a rate of 7% per year. Evan's favorite bread now costs $1.79.

This means that
`r = 0.07, P(0) = 1.79`. So

`P(t) = P(0)(1+r)^(t)`

`P(t) = 1.79(1+0.07)^(t)`

`P(t) = 1.79(1.07)^(t)`

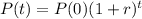
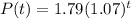
What did it cost 10 years ago?

`P(-10) = 1.79(1.07)^(-10) = 0.91`

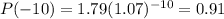
It cost $0.91 10 years ago.

How long before the cost of the bread doubles?

This is t for which P(t) = 2P(0) = 2*1.79. So

`P(t) = 1.79(1.07)^(t)`

`2*1.79 = 1.79(1.07)^(t)`

`(1.07)^(t) = 2`

`\log{(1.07)^(t)} = \log{2}`

`t\log{1.07} = \log{2}`

`t = \frac{\log{2}}{\log{1.07}}`

`t = 10.24`

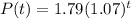
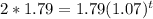
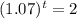
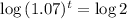
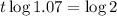
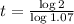
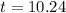
It takes 10.24 years for the cost of bread to double.