Answer:
Vx = 15V
Step-by-step explanation:
To find the speed of the third car you take into account that the distance that they travel is the same. Only time is different in one second. Mathematically you have:
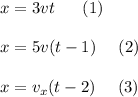
you equal the first and second equation obtain the time t:
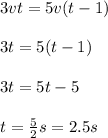
then, you can equal the third and first equation:
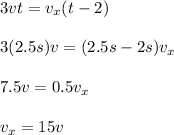
hence, Vx = 15V
- - - - - - - - - - - - - - - - - - -
TRANSLATION:
Para encontrar la velocidad del tercer automóvil, tenga en cuenta que la distancia que recorren es la misma. Solo el tiempo es diferente en un segundo. Matemáticamente tienes:
iguala la primera y segunda ecuación obtiene el tiempo t:
entonces, puedes igualar la tercera y primera ecuación:
por lo tanto, Vx = 15V