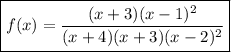Answer:
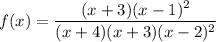
Explanation:
Each vertical asymptote corresponds to a zero in the denominator. When the function does not change sign from one side of the asymptote to the other, the factor has even degree. The vertical asymptote at x=-4 corresponds to a denominator factor of (x+4). The one at x=2 corresponds to a denominator factor of (x-2)², because the function does not change sign there.
__
Each zero corresponds to a numerator factor that is zero at that point. Again, if the sign doesn't change either side of that zero, then the factor has even multiplicity. The zero at x=1 corresponds to a numerator factor of (x-1)².
__
Each "hole" in the function corresponds to numerator and denominator factors that are equal and both zero at that point. The hole at x=-3 corresponds to numerator and denominator factors of (x-3).
__
Taken altogether, these factors give us the function ...