Question

A scientist created a scatterplot to display the height of a plant over a 12-day period. Plant Height A graph has days on the x-axis and height (inches) on the y-axis. A trend line goes through points (5, 3) and (12, 7). Which is the equation of the trend line that is shown? y = StartFraction 1 Over 7 EndFraction x + StartFraction 4 Over 7 EndFraction y = StartFraction 1 Over 7 EndFraction x + StartFraction 16 Over 7 EndFraction y = StartFraction 4 Over 7 EndFraction x minus StartFraction 1 Over 7 EndFraction y = StartFraction 4 Over 7 EndFraction x + StartFraction 1 Over 7 EndFraction

Answer 1

D

Explanation:

Answer 2

The correct option is (D)
`y=(4)/(7)\ x+(1)/(7)`.

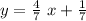Explanation:

The two-point form for the equation of straight line is:

`(y-y_(1))=(y_(2)-y_(1))/(x_(2)-x_(1))\ (x-x_(1))`

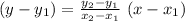
The two points provided are:

A = (5, 3)

B = (12, 7)

Compute the equation of the trend line as follows:

`(y-y_(1))=(y_(2)-y_(1))/(x_(2)-x_(1))\ (x-x_(1))\\\\(y-3)=(7-3)/(12-5)\ (x-5)\\\\(y-3)=(4)/(7)\ (x-5)\\\\y-3=(4)/(7)\ x-(20)/(7) \\\\y=(4)/(7)\ x-(20)/(7)+3\\\\y=(4)/(7)\ x+(-20+21)/(7)\\\\y=(4)/(7)\ x+(1)/(7)`

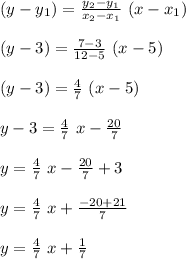
Thus, the equation of the trend line is
`y=(4)/(7)\ x+(1)/(7)`.

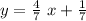The correct option is (D).