Answer:
The correct option is (D)
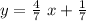 .
.
Explanation:
The two-point form for the equation of straight line is:
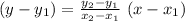
The two points provided are:
A = (5, 3)
B = (12, 7)
Compute the equation of the trend line as follows:
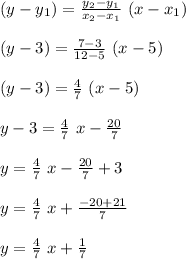
Thus, the equation of the trend line is
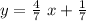 .
.
The correct option is (D).