Question

A surveyor holds a laser range finder 3 feet above the ground and determines that the range finder is 105 feet from a building and 121 feet from the top of the building. What is the height h of the building? Round your answer to the nearest tenth.

Answer 1

The height of the building is 63 ft

Explanation:

To solve this, we should note that the shape made by the range finder and the top and bottom of the building is a triangle.

Let the angle subtended by the range finder be
`\theta\\`

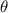
The height of the building can be got by Pythagoras theorem which shows

`hyp^(2) = opp^(2) + adj^(2)`

`121^(2)= 105^(2) + opp ^(2)`

`opp^(2)=121^(2)-105^(2)=3616`

`opp=√(3616) =60.133 \approx 60ft`

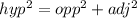
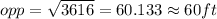
hence the height of the building is 3 ft + 60 ft = 63 ft