Question

Can someone help me with this? I need the answers so that i can direct my daughter on how to do it.

Answer 1

See explanation

Explanation:

A unit circle is simply a circle with the radius of one. This is important because a radian is the ratio of the radius to the circumference of a circle. If the radius is 1, then you don't need to worry about the radius and can focus just on the angles, since anything multiplied by 1 is just itself. This unit circle is divided up into 16 parts based on commonly used angle measures. Using right triangles, you can find the x and y coordinates of the points where these angle lines touch the edge of the circle with the pythagorean theorem (and these numbers have already been found for you in the first picture). Since this is a unit circle, the cosine of an angle yields the x coordinate of that angle's intersection with the edge of the circle, while the sine of an angle yields the y value. Therefore, for instance, in the first problem, you know that the cosine of an angle is 1/2, meaning that the x value of that angle is 1/2. You are also told that it is in the fourth quadrant, meaning that the only angle that corresponds to that is
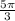`(5\pi)/(3)`. The sin of that angle, or the y value, is also written there and can be seen to be
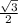`(√(3))/(2)`. I think you can solve the rest on your own, but comment if you need help!