Question

In HPE and GKJ, Which of the following would be enough to prove FPH ~ JKG?

Answer 1

Answer: Choice D

`(KJ)/(JG) = (PF)/(FH)`

======================================================

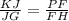
Step-by-step explanation:

Refer to the drawing below. I started off with the original diagram given, then I split up the triangles HPF (red) and GKJ (blue)

We're given that
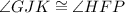`\angle GJK \cong \angle HFP`. If we had another congruent pair of angles, then we could use the AA (angle angle) similarity theorem to prove the triangles are similar. However, none of the answer choices mention another pair of congruent angles. Choices A and B are very close, but the
`\sim` should be
`\cong` instead. So we rule them out.

Focus on triangle GJK. Notice how the sides KJ and JG are surrounding the angle GJK. In other words, angle GJK is sandwiched between sides KJ and JG. Similarly, angle HFP is sandwiched between sides PF and FH in triangle HFP.

If we knew that the ratios KJ/JG and PF/FH were the same, then that would be enough info to use the SAS (side angle side) similarity theorem to prove the triangles similar. So that's why we go for
`(KJ)/(JG) = (PF)/(FH)`

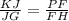
There are other possible ways to write that equation.