Answer:
The area of the shaded area is 27

Explanation:
The formula for the area of a circle is :
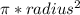
To work this out you would first have to work out the area of the circle. You can do this by multiplying
 by the radius of 6 squared, this gives you 36
by the radius of 6 squared, this gives you 36
 . However the question is asking for that section of the circle.
. However the question is asking for that section of the circle.
To work out the area of the shaded section you will first have to look at the missing angle, as it is 90° . A circle has 360° and so if we divide 360 by 90, this gives us 4. This tells us that
 of the circle is shaded as
of the circle is shaded as
 is not.
is not.
To work out the area of the shaded area you would divide the area of the whole circle which is 36
 by 4, this gives us 9
by 4, this gives us 9
 . This tells us the area of 1 quadrant of the circle.
. This tells us the area of 1 quadrant of the circle.
The next strep is to multiply 9
 by 3, this gives us 27
by 3, this gives us 27
 . This is because now that we know the area of one quadrant we can find the area of the shaded area which covers 3 quadrant of the circle.
. This is because now that we know the area of one quadrant we can find the area of the shaded area which covers 3 quadrant of the circle.
1) Multiply
 by 6 squared.
by 6 squared.
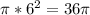
2) Divide 360 by 90.
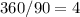
3) Divide 36
 by 4.
by 4.
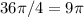
4) Multiply 9
 by 3.
by 3.
