Question

Two scientists decide to investigate the rate at which objects fall on different planets. They choose to use Earth and Mars as case studies. One scientist stays on Earth and the second goes to Mars. Each of them released a 2kg piece of stone at a height of 15 metres from the surface of the planet at exactly the same time. On which planet will the stone hit the ground first? Why do you think so?

Answer 1

the stones are released from rest at the same time, the stone that is on Earth to have more acceleration must first reach the ground

Step-by-step explanation:

For this exercise we will use the law of universal attraction on each planet and Newton's second law to calculate the body's acceleration on each planet

F = ma

F = G m M / r²

Where G is the universal gravitational constant, m the mass of the body, M the mass of the planet and r the distance

Let's start with the Earth

G m M / r² = m a

a = G M / r²

let's look for the distance

r =
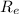`R_(e)` + h

a = G M / (R_{e} + h)² = (G M /R_{e}²) 1 /(1 + h /R_{e})² ²

as h << R_{e} we can expand this function

(1 + h /R_{e})⁻² = 1 -2 h / Re + ...

with h /R_{e} it is very small we can despise it

a = G M /R_{e}

the amount in parentheses is called the acceleration due to gravity

g = G M / R_{e}²

g = 6.67 10⁻¹¹ 5.98 10²⁴ / (6.37 10⁶)²

g = 9.8 m / s ²

Now let's calculate the acceleration on Mars, let's use index 2 for this planet

a = G M2 / R_{2}²

a = 6.67 10⁻¹¹ 6.42 10²³ / (3.37 10⁶)

a = 3.77 m / s²

Let's analyze these results as the stones are released from rest at the same time, the stone that is on Earth to have more acceleration must first reach the ground

we can use the equation

y = v₀ t - ½ to t2

v₀ = 0

t = √ (2y / a)

we see that as the acceleration is greater the time decreases