Question

Find the frequency of the 4th harmonic waves on a violin string that is 48.0cm long with a mass of 0.300 grams

and is under a tension of 4.00N. ​

Answer 1

The frequency of the 4th harmonic of the string is 481.13 Hz.

Step-by-step explanation:

When a stretch string fixed at both ends is set into vibration, it produces its lowest sound of possible note called the fundamental frequency. Under certain conditions on the string, higher frequencies called harmonics or overtones can be produced.

The frequency of the forth harmonic is the third overtone of the string and can be determined by:

f =
`(2)/(L)`
`\sqrt{(T)/(m) }`

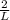
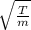
Given that; L = 48.0 cm = 0.48 m,

m = 0.3 g = 0.0003 Kg,

T = 4.0 N,

f =
`(2)/(0.48)`
`\sqrt{(4)/(0.0003) }`

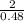
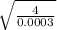
f = 4.1667 × 115.4701

= 481.1252

f = 481.13 Hz

The frequency of the 4th harmonic of the string is 481.13 Hz.