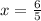Answer: This took me a long time to type, hope you read it and find it helpful and easy to understand...
1.

2.
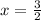
3.

4.
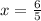
Explanation:
1.
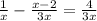
To make it easier to add / subtract fractions, we are looking for common denominators. I can see that if I move the fraction on the left with a denominator 3x to the right, I'll be able to add two equations with like denominator.
Let's add
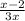
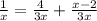
Add the numerators and keep the same denominator.
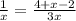

To get rid of the denominator x on the left side, we can multiply by x.
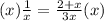
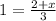
Now multiply by 3.

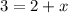
Subtract 2.
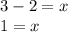
The value of x is 1.
Proof.
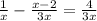
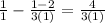
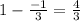
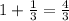

I can't show the proof to the following problems because I have a 5000 character limit.
-----------------------------------------------------------------------------------------
2.
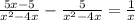
Again, we have like denominators, therefore, we can simply subtract the numerators and keep the same denominator.
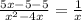
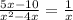
Again, we can multiply by x to get rid of the x in the denominator.

Do not distribute the x in the numerator yet because we're gonna eliminate it later.
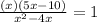
Factor the denominator.
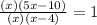
Simplify x's.
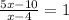
Multiply by x-4 to get rid of the denominator.
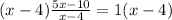

Add 10

Subtract x
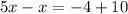
Combine like terms;
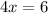
Divide by 4.
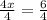
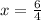
Simplify by 2.
6/2 = 3
4/2 = 2
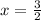
-----------------------------------------------------------------------
3.

Same denominator, add numerators.
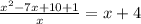
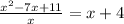
Multiply by x to get rid of the x.
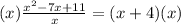
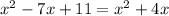
Subtract
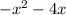
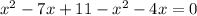
Combine like terms;
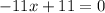
Subtract 11.
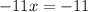
Divide by -11
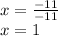
-------------------------------------------------------------------------
4.
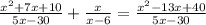
It's easier if you move the operation with denominator x+6 to the right side with negative sign and bring the operation on the right side to the left side with negative sign as well.
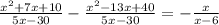
Now, since we have the same denominators, we can simply subtract numerators.

Distribute the negative sign.
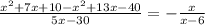
Combine like terms;
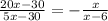
Factor.
I can see that I can factor a 5 on both numerator and numerator. This will allow me to simplify them.
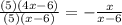
Simplify.
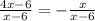
Multiply by x-6
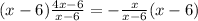
This will simplify the denominators.
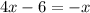
Add x and 6.
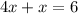
Combine like terms;
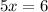
Divide by 5.