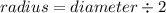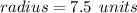Answer:
The value of radius is 7.5 units
Explanation:
Given that a line that pass through the origin and form a triangle is a right-angle triangle. So in order to find the diameter/hypotenuse, you have to use Pythogaras Theorem :
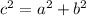
Let a = 12 units,
Let b = 9 units,
Let c = hypo.,
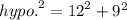
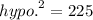

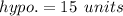
We have found out that the hypotenuse of the triangle is the diameter of circle. So in order to find radius, you have to divide it by 2 :