The value of
 is 50 degrees, which corresponds to option D.
is 50 degrees, which corresponds to option D.
The diagram shows a circle circumscribed around quadrilateral ABCD, with an angle at C that is 130 degrees. Assuming that ABCD is a cyclic quadrilateral (a quadrilateral whose vertices all lie on the circumference of a circle), then the opposite angles of a cyclic quadrilateral sum up to 180 degrees due to the Inscribed Angle Theorem. This theorem states that the opposite angles of a cyclic quadrilateral are supplementary.
Given that angle
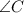 is 130 degrees, we can find the measure of angle
is 130 degrees, we can find the measure of angle
 by the following relationship for a cyclic quadrilateral:
by the following relationship for a cyclic quadrilateral:
![\[ \angle A + \angle C = 180^\circ \]](https://img.qammunity.org/2021/formulas/mathematics/college/if9ev4e6bn7d5wfkz2gm8hgpnfd2tttpzp.png)
Plugging in the value for
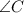 , we get:
, we get:
![\[ \angle A + 130^\circ = 180^\circ \]](https://img.qammunity.org/2021/formulas/mathematics/college/ldnymbhjhp6qxxt4dar7i6p8wg22x98ify.png)
Now, let's calculate the value of angle
 :
:
![\[ \angle A = 180^\circ - 130^\circ \]](https://img.qammunity.org/2021/formulas/mathematics/college/9z4gfv8zlnzzv0rhabaqb25uiy9ylbsqfq.png)
![\[ \angle A = 50^\circ \]](https://img.qammunity.org/2021/formulas/mathematics/college/bnv4u3qmkz4a8icg9293ehv2apwh17ix8a.png)
Therefore, The answer is 50 degrees.