Complete Question
A 0.025-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 150 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is x = 0.024 m, what is the kinetic energy of the block?
Answer:
The kinetic energy is
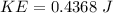
Step-by-step explanation:
From the question we are told that
The mass of the block is
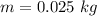
The spring constant is
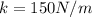
The length of first displacement is
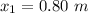
The length of first displacement is
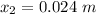
At the
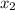 the kinetic energy is mathematically evaluated as
the kinetic energy is mathematically evaluated as

Where
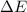 is the change in energy stored on the spring which is mathematically represented as
is the change in energy stored on the spring which is mathematically represented as
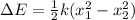
=>

Substituting value