Answer:
7v - 5u
Explanation:
Our expression is:
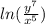 . Remember the property of ln, where ln(a / b) = ln(a) - ln(b). We can apply that here:
. Remember the property of ln, where ln(a / b) = ln(a) - ln(b). We can apply that here:
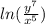 = ln(
= ln(
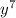 ) - ln(
) - ln(
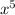 )
)
Now, also remember that when we have ln(
 ), we can write it as b * ln(a). Apply this here:
), we can write it as b * ln(a). Apply this here:
ln(
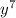 ) = 7ln(y)
) = 7ln(y)
ln(
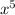 ) = 5ln(x)
) = 5ln(x)
Notice that since u = ln(x) and v = ln(y), we can replace those respectively:
7ln(y) = 7v
5ln(x) = 5u
Put it together:
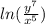 = 7v - 5u
= 7v - 5u