Question

Write the equation of the line in slope-intercept form of the line that passes through the points (1,6) and (3,-4).

A. y=11x-5
B. y=3x-4
C. y=x+6
D. y=-5x+11

Answer 1

Option D

Explanation:

Slope-intercept form is:
`y=mx+b`

We first need to find the slope of the line with the points (1,6) and (3, -4).

`\text {Use the slope formula: }\\m = (y_2-y_1)/(x_2-x1) =(-4-6)/(3-1) = (-10)/(2) = -5`

The slope (or m) is -5.

With this information, we can eliminate A, B, and C, because in the equation the slope is not -5.

D looks promising. Let's make sure that it is correct by finding the y-intercept.

`y = -5x + b\\\text {Using the point: (1,6)}\\\\\rightarrow 6 = -5(1) + b\\\\6 = -5 + b\\6+5 = (-5 + 5) +b\\11 = b`

The y-intercept is 11.

So, the equation of the line in slope-intercept form of the line that passes through the points (1,6) and (3,-4) should be
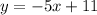`y=-5x+11`, or Option D.