Question

Find each of the following indefinite integrals.


∫sec^2 θ √ tanθ dθ

Answer 1

`\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta = \frac{2[tan(\theta)]^\bigg{(3)/(2)}}{3} + C`

General Formulas and Concepts:

Algebra I

• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Differentiation

• Derivatives
• Derivative Notation

Integration

• Integrals
• Indefinite Integrals
• Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

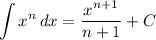
U-Substitution

Explanation:

Step 1: Define

Identify

`\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta`

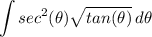
Step 2: Integrate Pt. 1

1. [Integrand] Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta = \int {sec^2(\theta)[tan(\theta)]^\bigg{(1)/(2)}} \, dx`

Step 3: Integrate Pt. 2

Identify variables for u-substitution.

1. Set u:
   `\displaystyle u = tan(\theta)`
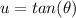
2. [u] Differentiate [Trigonometric Differentiation]:
   `\displaystyle du = sec^2(\theta) \ d\theta`

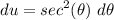
Step 4: Integrate Pt. 3

1. [Integral] U-Substitution:
   `\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta = \int {u^\bigg{(1)/(2)}} \, du`
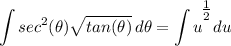
2. [Integral] Reverse Power Rule:
   `\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta = \frac{2u^\bigg{(3)/(2)}}{3} + C`
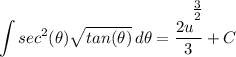
3. Back-Substitute:
   `\displaystyle \int {sec^2(\theta)√(tan(\theta))} \, d\theta = \frac{2[tan(\theta)]^\bigg{(3)/(2)}}{3} + C`

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e