Answer:
1. x² - 16x = -12
2. x² - 16x + 64 = -12 + 64
3. (x - 8)² = 52
4. x - 8 = ± √52
5. x = 8 ± √52
6. x = 8 ± 2√13
Explanation:
1. Move the constant to the other side of the equation:
x² - 16x +12-12 = 0-12
x² - 16x = -12
2. Find the new value of c by using the formula
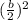
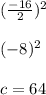
3. Plug the new value of c into the equation. Make sure to add it to both sides of the equation, because if you do something to one side, you must do it to the other:
x² - 16x + 64 = -12 + 64
x² - 16x + 64 = 52
4. Form a perfect sqaure by factoring -16 and 64 by figuring out two numbers that have a sum of -16 and a product of 64:
-8 + (-8) = -16
-8 · (-8) = 64
(x - 8)²
Plugging this into the equation:
(x - 8)² = 52
5. Take the square root of both sides:
√(x - 8)² = √52
x - 8 = √52
6. Isolate x:
x - 8+8 = 2√52+8
x = 8 ± 2√52
52 can be squared, so:
x = 8 ± 2√13
hope this helps!