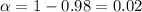Question

A company surveyed 2400 men where 1248 of the men identified themselves as the primary grocery shopper in their household. ​a) Estimate the percentage of all males who identify themselves as the primary grocery shopper. Use a 98​% confidence interval. Check the conditions first. ​b) A grocery store owner believed that only 43​% of men are the primary grocery shopper for their​ family, and targets his advertising accordingly. He wishes to conduct a hypothesis test to see if the fraction is in fact higher than 43​%. What does your confidence interval​ indicate? Explain. ​c) What is the level of significance of this​ test? Explain.

Answer 1

a) With a confidence level of 98%, the percentage of all males who identify themselves as the primary grocery shopper are between 0.4962 and 0.5438.

b) The lower limit of the confidence interval is higher that 0.43, so if he conduct a hypothesis test, he will find that the data shows evidence to said that the fraction is higher than 43%.

c)
`\alpha =1-0.98=0.02`

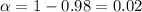
Explanation:

If np' and n(1-p') are higher than 5, a confidence interval for the proportion is calculated as:

`p'-z_(\alpha/2)\sqrt{(p'(1-p'))/(n) }\leq p\leq p'+z_(\alpha/2)\sqrt{(p'(1-p'))/(n) }`

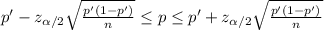
Where p' is the proportion of the sample, n is the size of the sample, p is the proportion of the population and
`z_(\alpha/2)` is the z-value that let a probability of
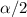`\alpha/2` on the right tail.

Then, a 98% confidence interval for the percentage of all males who identify themselves as the primary grocery shopper can be calculated replacing p' by 0.52, n by 2400,
`\alpha` by 0.02 and
`z_(\alpha/2)` by 2.33

Where p' and
`\alpha` are calculated as:

`p' = (1248)/(2400)=0.52\\\alpha =1-0.98=0.02`

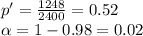
So, replacing the values we get:

`0.52-2.33\sqrt{(0.52(1-0.52))/(2400) }\leq p\leq 0.52+2.33\sqrt{(0.52(1-0.52))/(2400) }\\0.52-0.0238\leq p\leq 0.52+0.0238\\0.4962\leq p\leq 0.5438`

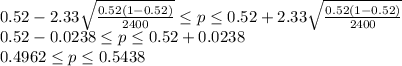
With a confidence level of 98%, the percentage of all males who identify themselves as the primary grocery shopper are between 0.4962 and 0.5438.

The lower limit of the confidence interval is higher that 0.43, so if he conduct a hypothesis test, he will find that the data shows evidence to said that the fraction is higher than 43%.

Finally, the level of significance is the probability to reject the null hypothesis given that the null hypothesis is true. It is also the complement of the level of confidence. So, if we create a 98% confidence interval, the level of confidence
`1-\alpha` is equal to 98%

It means the the level of significance
`\alpha` is:

`\alpha =1-0.98=0.02`