Question

A company produces two models of a​ surfboard: a standard model and a competition model. If the standard model is produced at a variable cost of ​$240 each and the competition model at a variable cost of ​$330 ​each, and if the total fixed costs per month are ​$4 comma 000​, then the monthly cost function is given by Upper C (x comma y )equals 4 comma 000 plus 240 x plus 330 y where x and y are the numbers of standard and competition models produced per​ month, respectively. Find ​C(24​,12​), ​C(70​,7​), and ​C(30​,30​).

Answer 1

(1) C (24, 12) = $13,720

(2) C (70, 7) = $23,110

(3) C (30, 30) = $21,100

Explanation:

The monthly cost function for the production of two models of a​ surfboard, a standard model and a competition model is:

`C(x,\ y)=4000+240x+330y`

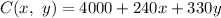
Here,

x = number of standard model surfboard produced per​ month

y = number of competition model surfboard produced per​ month

(1)

Compute the value of C (24, 12) as follows:

`C(x,\ y)=4000+240x+330y`

`C(24,\ 12)=4000+(240 \cdot24)+ (330\cdot12)`

`=4000+5760+3960\\=13720`

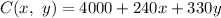
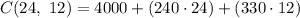
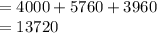
Thus, the monthly cost of producing 24 standard model and 12 competition model surfboard per month is $13,720.

(2)

Compute the value of C (70, 7) as follows:

`C(x,\ y)=4000+240x+330y`

`C(70,\ 7)=4000+(240 \cdot70)+ (330\cdot7)`

`=4000+16800+2310\\=23110`

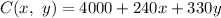
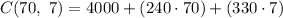
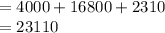
Thus, the monthly cost of producing 70 standard model and 7 competition model surfboard per month is $23,110.

(3)

Compute the value of C (30, 30) as follows:

`C(x,\ y)=4000+240x+330y`

`C(30,\ 30)=4000+(240 \cdot30)+ (330\cdot30)`

`=4000+7200+9900\\=21100`

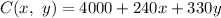
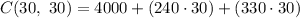
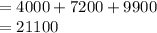
Thus, the monthly cost of producing 30 standard model and 30 competition model surfboard per month is $21,100.