Question

A nonprofit organization sent mailing labels along with a request for donations to a random sample of 75,000 potential donors on their mailing list and received 5625 donations from the effort. In the past, the organization has had a contribution rate of 6%, but the director of the program hoped that the addition of the mailing labels would increase that rate. Perform a hypothesis test using α=0.05. Be sure to include the following: State the null and alternative hypotheses in symbols and words. Assume conditions have been met. (2 pts.) Perform your hypothesis test "by hand" using the equation editor. Be sure to use the appropriate probability notation. Don't write your conclusion in this step.(4 pts.) Construct a 90% confidence interval, again showing calculations "by hand". Don't write your conclusion in this step. (4 pts.) State your FULL conclusion making sure to site whether we reject or fail to reject and what that means in context based on the p-value. Then support your conclusion with the results from your confidence interval. Then be sure to note whether the hypothesized value falls in our interval and what that means. (3 pts.)

Answer 1

Check the explanation

Explanation:

The null and alternative hypotheses in symbols and words are as follows:

: p ≤ 0.06 (There has been no change in the contribution rate due to addition of the mailing labels)

: p > 0.06 (The addition of the mailing labels has increased the contribution rate)

Test Statistics

The following information is provided: The sample size is N = 75000, the number of favorable cases is X = 5625, and the sample

The z-statistic is computed as follows:

-
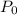`P_0` (1 -

Test statistic z = 17.297

P-value

P-value corresponding to z = 17.297 for a two tailed test is obtained using standard normal table.

p-value = 0.0000

90% Confidence Interval Calculation

Kindly check the attached image below.

Conclusion

Since p-value = 0.0000 < α = 0.05, we reject null hypothesis .

At 0.05 significance level, there is enough evidence to conclude that the addition of the mailing labels has increased the contribution rate.

Since the 90% confidence interval (0.073, 0.077) does not contain the hypothesized value 0.06, the result is significant and we reject null hypothesis.

In other words, at 0.10 significance level, there is enough evidence to conclude that the addition of the mailing labels has increased the contribution rate.