Question

Based on an indication that mean daily car rental rates may be higher for Boston than for Dallas, a survey of eight car rental companies in Boston is taken and the sample mean car rental rate is $47, with a standard deviation of $3. Further, suppose a survey of nine car rental companies in Dallas results in a sample mean of $44 and a standard deviation of $3. Use alpha = 0.05 to test to determine whether the average daily car rental rates in Boston are significantly higher than those in Dallas. Assume car rental rates are normally distributed and the population variances are equal. The degrees of freedom for this problem are _______.

Answer 1

`t=\frac{(47 -44)-(0)}{3\sqrt{(1)/(8)+(1)/(9)}}=2.058`

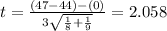
The degrees of freedom are:

`df=8+9-2=15`

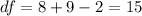
And the p value would be:

`p_v =P(t_(15)>2.058) =0.0287`

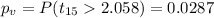
Since we have a p value lower than the significance level given of 0.05 we can reject the null hypothesis and we can conclude that the true mean for car rental rates in Boston are significantly higher than those in Dallas

Explanation:

Data given

`n_1 =8` represent the sample size for group Boston

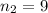`n_2 =9` represent the sample size for group Dallas

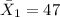`\bar X_1 =47` represent the sample mean for the group Boston

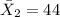`\bar X_2 =44` represent the sample mean for the group Dallas

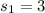`s_1=3` represent the sample standard deviation for group Boston

`s_2=3` represent the sample standard deviation for group Dallas

We can assume that we have independent samples from two normal distributions with equal variances and that is:

`\sigma^2_1 =\sigma^2_2 =\sigma^2`

Let the subindex 1 for Boston and 2 for Dallas we want to check the following hypothesis:

Null hypothesis:
`\mu_1 \leq \mu_2`

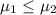
Alternative hypothesis:
`\mu_1 > \mu_2`

The statistic is given by this formula:

`t=\frac{(\bar X_1 -\bar X_2)-(\mu_(1)-\mu_2)}{S_p\sqrt{(1)/(n_1)+(1)/(n_2)}}`

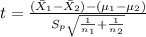
Where t follows a t student distribution with
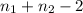`n_1+n_2 -2` degrees of freedom and the pooled variance
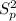`S^2_p` is given by this formula:

`\S^2_p =((n_1-1)S^2_1 +(n_2 -1)S^2_2)/(n_1 +n_2 -2)`

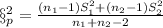
Replacing we got:

`\S^2_p =((8-1)(3)^2 +(9 -1)(3)^2)/(8 +9 -2)=9`

And the deviation would be just the square root of the variance:

`S_p=3`

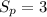
The statitsic would be:

`t=\frac{(47 -44)-(0)}{3\sqrt{(1)/(8)+(1)/(9)}}=2.058`

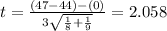
The degrees of freedom are:

`df=8+9-2=15`

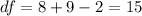
And the p value would be:

`p_v =P(t_(15)>2.058) =0.0287`

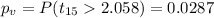
Since we have a p value lower than the significance level given of 0.05 we can reject the null hypothesis and we can conclude that the true mean for car rental rates in Boston are significantly higher than those in Dallas