Question

In 2008, data from the Center for Disease Control revealed that 28.5% of all male teenagers, aged 18-19 and attending U.S. colleges were overweight. The definition of overweight is a body mass index (BMI) of over 25.

In 2019, a professor in public health at a major university wanted to determine whether that proportion had decreased since 2008. So, he sampled 800 randomly selected incoming male freshman at universities around the country. Using the BMI measurements, he found that 210 of them were overweight. Test the professor’s claim at an α = 0.05 level of significance, the proportion of obese male teenagers in American colleges decreased. Make sure that any necessary assumptions for conducting the hypothesis test are satisfied.
A) State the null and alternative hypothesis.
H0:
Ha:
B) Determine the critical value(s) for the test.
C) Compute the test statistic (show your work).
D) Make your decision.
E) State your conclusion in terms of the professor’s claim.

Answer 1

a) H0 : u = 28.5%

H1 : u < 28.5%

b) critical value = - 1.645

c) test statistic Z= - 1.41

d) Fail to reject H0

e) There is not enough evidence to support the professor's claim.

Explanation:

Given:

P = 28.5% ≈ 0.285

X = 210

n = 800

`p' = (X)/(n) = (210)/(800) = 0.2625`

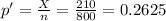
Level of significance = 0.05

a) The null and alternative hypotheses are:

H0 : u = 28.5%

H1 : u < 28.5%

b) Given a 0.05 significance level.

This is a left tailed test.

The critical value =

`-Z_0.05 = -1.645`

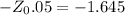
The critical value = -1.645

c) Calculating the test statistic, we have:

`Z = \frac{p' - P}{\sqrt{(P(1-P))/(n)}}`

`Z = \frac{0.2625 - 0.285}{\sqrt{(28.5(1-28.5))/(800)}}`

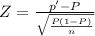
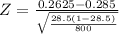
Z = -1.41

d) Decision:

We fail to reject null hypothesis H0, since Z = -1.41 is not in the rejection region, <1.645

e) There is not enough evidence to support the professor's claim that the proportion of obese male teenagers decreased.