Question

The graph below shows the height of a projectile seconds after it is launched. If acceleration due to gravity is -16 ft/s^2 which

equation models the height of the projectile correctly?
h(t)=at^2+vt+h0

Answer 1

D on edge 2021 ;))

Explanation:

Answer 2

The equation is:

`h(t)=-16t^2+32t+5`

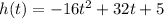
Explanation:

We have the height of the projectile graphed, in function of time. The acceleration due to gravity is a=-16 ft/s^2.

We have the equation

`h(t)=at^2+vt+h_0`

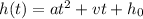
and we have to calculate the parameters a, v and h0 to define the equation that corresponds to the graphed heigth.

The value h0 can be seen in the graph, as is the value h(t=0)=5.

We know also, that the acceleration is a=-16 ft/s^2.

The maximum height is reached at t=1 and has a height of of h(1)=21.

We can relate this maximum value by deriving the equation and equal to zero:

`(dh)/(dt)=2at+v=0\\\\\\v=-2at\\\\t=1,a-16\rightarrow v=-2\cdot (-16)\cdot1=32`

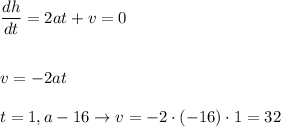
The equation is then:

`h(t)=-16t^2+32t+5`

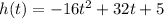
Note: the time when the projectile lands (h=0) is not exactly t=2.15, it is a rounded value.