Answer:
The equation is:
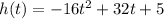
Explanation:
We have the height of the projectile graphed, in function of time. The acceleration due to gravity is a=-16 ft/s^2.
We have the equation

and we have to calculate the parameters a, v and h0 to define the equation that corresponds to the graphed heigth.
The value h0 can be seen in the graph, as is the value h(t=0)=5.
We know also, that the acceleration is a=-16 ft/s^2.
The maximum height is reached at t=1 and has a height of of h(1)=21.
We can relate this maximum value by deriving the equation and equal to zero:
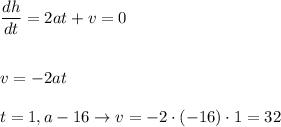
The equation is then:
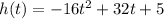
Note: the time when the projectile lands (h=0) is not exactly t=2.15, it is a rounded value.