Question

Sheer industries is considering a new computer-assisted program to train maintenance employees to do machine repairs. In order to fully evaluate the program, the director of manufacturing requested an estimate of the population mean time required for maintenance employees to complete the computer assisted training. Use 7.64 days as a planning value for the population standard deviation. (Round your answers up to the nearest whole number.)

(a) Assuming 95% confidence, what sample size would be required to obtain a margin of error of 0.5 days?
(b) If the precision statement was made with 90% confidence, what sample size would be required to obtain a margin of error of 3 days?

Answer 1

a) The sample size 'n' = 896.93≅ 897

b) The sample size n = 17.54

Explanation:

Step(i):-

a) Given the margin of error (M.E) = 0.5 days

Given population standard deviation (σ) = 7.64

The tabulated value
`Z_{(\alpha )/(2) } = Z_{(0.05)/(2) }= Z_(0.025) = 1.96`

The margin of error is determined by

M.E =
`\frac{Z_{(\alpha )/(2) } S.D}{√(n) }`

`0.5 = (1.96 X 7.64)/(√(n) )`

`√(n) = (1.96 X 7.64)/(0.5)`

`√(n) = 29.94`

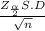
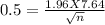
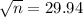
Squaring on both sides, we get

n = 896.93

The sample size 'n' = 896.93

Step(ii):-

b)

Given the margin of error (M.E) = 3 days

Given population standard deviation (σ) = 7.64

The tabulated value
`Z_{(\alpha )/(2) } = Z_{(0.10)/(2) }= Z_(0.05) = 1.645`

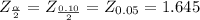
The margin of error is determined by

M.E =
`\frac{Z_{(\alpha )/(2) } S.D}{√(n) }`

`3 = (1.645 X 7.64)/(√(n) )`

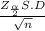
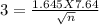
Cross multiplication , we get

`√(n) = (1.645 X 7.64)/(3)`

`√(n) = 4.189`

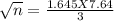
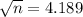
Squaring on both sides, we get

n = 4.189 X 4.189

The sample size n = 17.54

Conclusion:-

a) The sample size 'n' = 896.93≅ 897

b) The sample size n = 17.54