Question

A farmer who grows genetically engineered corn is experiencing trouble with corn borers. A random check of 5,000 ears revealed the following: many of the ears contained no borers. Some ears had one borer; a few had two borers; and so on. The distribution of the number of borers per ear approximated the Poisson distribution. The farmer counted 3,500 borers in the 5,000 ears. What is the probability that an ear of corn selected at random will contain no borers? 0.3476 0.4966 1.000 0.0631

Answer 1

Probability that an ear of corn selected at random will contain no borers is 0.4966.

Explanation:

We are given that the distribution of the number of borers per ear approximated the Poisson distribution. The farmer counted 3,500 borers in the 5,000 ears.

Let X = Number of borers per ear

The probability distribution of the Poisson distribution is given by;

`P(X=x) = (e^(-\lambda )* \lambda^(x) )/(x!) ; x = 0,1,2,3,......`

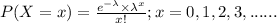
where,
`\lambda` = parameter of this distribution and in our question it is proportion of bores in the total ears =
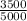`(3500)/(5000)` = 0.7

SO, X ~ Poisson(
`\lambda` = 0.7)

Now, probability that an ear of corn selected at random will contain no borers is given by = P(X = 0)

P(X = 0) =
`(e^(-0.7)* 0.7^(0) )/(0!)`

=
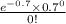
`e^(-0.7)` = 0.4966

Hence, the required probability is 0.4966.