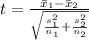Answer:
Explanation:
H0: µ1 – µ2 = 0
HA: µ1 – µ2 ≠ 0
We have given,
The population variances are not known and cannot be assumed equal.
The test statistic for the test is
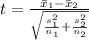
Where,
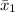 = sample meaan of population 1
= sample meaan of population 1
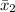 = sample mean of population 2
= sample mean of population 2
 = sample size of population 1
= sample size of population 1
 = sample size of population 2
= sample size of population 2
Therefore, this is the test