Question

Suppose the probability of an athlete taking a certain illegal steroid is 10%. A test has been developed to detect this type of steroid and will yield either a positive or negative result. Given that the athlete has taken this steroid, the probability of a positive test result is 0.995. Given that the athlete has not taken this steroid, the probability of a negative test result is 0.992. Given that a positive test result has been observed for an athlete, what is the probability that they have taken this steroid

Answer 1

93.25% probability that they have taken this steroid

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

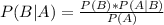
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Positive test

Event B: Taking the steroid.

Suppose the probability of an athlete taking a certain illegal steroid is 10%.

This means that
`P(B) = 0.1`

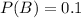
Given that the athlete has taken this steroid, the probability of a positive test result is 0.995.

This means that
`P(A|B) = 0.995`

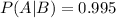
Positive test:

99.5% of 10%(If the athlete has taken).

100-99.2 = 0.8% of 100-10 = 90%(Athlete has not taken)

Then

`P(B) = 0.995*0.1 + 0.008*0.9 = 0.1067`

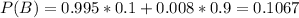
Given that a positive test result has been observed for an athlete, what is the probability that they have taken this steroid

`P(B|A) = (P(B)*P(A|B))/(P(A)) = (0.1*0.995)/(0.1067) = 0.9325`

93.25% probability that they have taken this steroid