Question

Two rectangular prisms, M and N, are mathematically similar. The volumes of M and N are 17 cm^3 and 136 cm^3, respectively. The height of N is 18 cm. Find the corresponding height of M.

Answer 1

We have been given that two rectangular prisms, M and N, are mathematically similar. The volumes of M and N are 17 cm^3 and 136 cm^3, respectively. The height of N is 18 cm. We are asked to find the height of M.

First of all, we will find the ratio between sides of rectangle M and N using proportions.

`\frac{\text{Side of N}}{\text{Side of M}}=\frac{\text{ Volume of N}}{\text{ Volume of M}}`

`\frac{\text{Side of N}}{\text{Side of M}}=\frac{136\text{ cm}^3}{17\text{ cm}^3}`

`\frac{\text{Side of N}}{\text{Side of M}}=\frac{8\text{ cm}^3}{1\text{ cm}^3}`

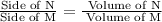
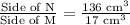
Now we will take cube root on right side to find length in cm.

`\frac{\text{Side of N}}{\text{Side of M}}=\frac{\sqrt[3]{\text{8 cm}^3}}{\sqrt[3]{\text{1 cm}^3}}`

`\frac{\text{Side of N}}{\text{Side of M}}=\frac{\text{2 cm}}{\text{1 cm}}`

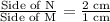
Therefore, sides of rectangle N is 2 times greater than sides of rectangle M.

To find height of rectangle M, we will divide side of rectangle N by 2.

`\text{Height of rectangle M}=(18)/(2)=9`

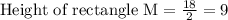
Therefore, height of rectangle M is 9 cm.