Question

Researchers wondered if there was a difference between males and females in regard to some common annoyances. They asked a random sample of males and​ females, the following​ question: "Are you annoyed by people who repeatedly check their mobile phones while having an​ in-person conversation?" Among the 530 males​ surveyed, 175 responded​ "Yes"; among the 575 females​ surveyed, 218 responded​ "Yes." Does the evidence suggest a higher proportion of females are annoyed by this​ behavior? Complete parts​ below.

(a) Determine the sample proportion for each sample.

The proportions of the females and males who took the survey who are annoyed by the behavior in question are ____and _____ respectively. (Round to four decimal places as needed.)

(b) Explan why this study can be analyzed using the methods for conducting a hypothesis test regarding two independent proportions. Select all that apply.

A. The sample size is more than 5% of the population size for each sample
B. The sample size is less than 5% of the population size for each sample
C. The samples are dependent.
D. The data come from a population that is nornally distributed.
E. np (1-) 10 and n2p2 (1-2) 210
F. The samples are independent.

(c) What are the null and alternative hypotheses? Let p1 represent the population proportion of females who are annoyed by the behavior in question and p2 represent the population proportion of males who are annoyed by the behavior in question.

Answer 1

a)

The proportions of the females and males who took the survey who are annoyed by the behavior in question are 0.3301 and_0.3791 respectively

b)

D) The data come from a Population that is Normally distributed

F) the samples are independent

c)

Null hypothesis: H₀:
`p_(m) ^(-) - p^(-) _(fm) \leq 0`

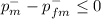
Alternative Hypothesis H₁:
`p_(m) ^(-) - p^(-) _(fm) \geq 0`

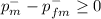
Explanation:

Given data Among the 530 males​ surveyed, 175 responded​ "Yes

The sample proportion of males

`p_(m) ^(-) = (x)/(n) = (175)/(530) = 0.3301`

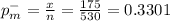
The sample proportion of 575 Females surveyed, 218 responded​ "Yes

`p_(fem) ^(-) = (x)/(n) = (218)/(575) = 0.3791`

a)

The proportions of the females and males who took the survey who are annoyed by the behavior in question are 0.3301 and_0.3791 respectively

b)

The data come from a Population that is normally distributed.

The two samples are independent

c)

Null hypothesis: H₀:
`p_(m) ^(-) - p^(-) _(fm) \geq 0`

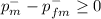
Alternative Hypothesis H₁:
`p_(m) ^(-) - p^(-) _(fm) \leq 0`

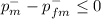
We will use two samples Z - hypothesis test

`Z = (p^(-) _(m) - p^(-) _(fem) )/(se(p^(-) _(m)-p^(-) _(fem) ) )`

`Se(p_(m) -p_(fem)) = \sqrt{(p_(m)(1-p_(m)) )/(n_(m) )+(p_(fem) (1-p_(fem) ))/(n_(fem) ) }`

`Se(p_(m) -p_(fem)) = \sqrt{(0.3301(1-0.3301) )/(530 )+(0.3791(1-0.3791))/(575) }`

`Se(p_(m) ^(-) - p^(-) _(fem) ) = √(0.000826) = 0.0287`

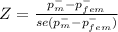
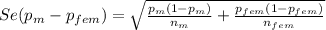
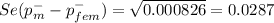
The test statistic

`Z = (0.3301-0.3791)/(0.02875)`

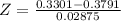
Z = -1.7043

|Z| = |-1.7043|

The tabulated value Z₀.₉₅ = 1.96

The calculated Z= 1.7043 < 1.96 at 0.05 level of significance

The null hypothesis is accepted

Conclusion:-

The evidence suggest not a higher proportion of females are annoyed by this​ behavior