Question

For each exam, Ariadne studies with probability 1/2 and does not study with probability 1/2 , independently of any other exams. On any exam for which she has not studied, she still has a 0.20 probability of passing, independently of whatever happens on other exams. What is the expected number of total exams taken until she has had 3 exams for which she did not study but which she still passed?

Answer 1

The expected number of total exams taken until she has had 3 exams for which she did not study but which she still passed is 15.

Explanation:

For each exam that she has not studied, there are only two possible outcoes. Either she passed, or she did not. The probability of passing on any of these exams is independent of other exams. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected number of trials for q sucesses is:

`E(X) = (q)/(p)`

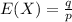
On any exam for which she has not studied, she still has a 0.20 probability of passing, independently of whatever happens on other exams.

This means that
`p = 0.2`

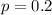
What is the expected number of total exams taken until she has had 3 exams for which she did not study but which she still passed?

3 exams, so q = 3.

`E(X) = (q)/(p) = (3)/(0.2) = 15`

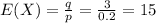
The expected number of total exams taken until she has had 3 exams for which she did not study but which she still passed is 15.