Question

A card is selected randomly from a jar that contains 15 cards, numbered from 25 to 39. What is the probability that the card selected bears a number less than 34? Give your answer as a decimal.

Answer 1

The probability that the card selected bears a number less than 34 is 0.3333.

Explanation:

Let random variable X be defined as the number on the selected card.

There are N = 15 total cards.

The number on the cards are as follows:

S = {25, 26, 27,..., 38, 39}

The probability of an event, E is the ratio of the number of favorable outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

In this case we need to compute the probability that the card selected bears a number less than 34.

The favorable outcomes are:

s = {25, 36, 37, 38, 39}

n (X < 34) = 5

Compute the probability that the card selected bears a number less than 34 as follows:

`P(X<34)=(n(X<34))/(N)`

`=(5)/(15)\\\\=(1)/(3)\\\\=0.3333`

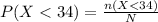
Thus, the probability that the card selected bears a number less than 34 is 0.3333.