Question

The quality control manager at a light bulb factory needs to estimate the mean life of a batch (population) of light bulbs. We assume that the population standard deviation is 100 hours. A random sample of 64 light bulbs from the batch yields a sample mean of 350. a) Construct a 95% confidence interval for the population mean of light bulbs in this batch. b) Do you think that the manufacturer has the right to state that the average life of the light bulbs is 400 hours

Answer 1

a)95% confidence intervals for the population mean of light bulbs in this batch

(325.5 ,374.5)

b)

The calculated value Z = 4 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

The manufacturer has not right to take the average life of the light bulbs is 400 hours.

Explanation:

Given sample size n = 64

Given mean of the sample x⁻ = 350

Standard deviation of the Population σ = 100 hours

The tabulated value Z₀.₉₅ = 1.96

95% confidence intervals for the population mean of light bulbs in this batch

`(x^(-) - Z_{(\alpha )/(2) } (S.D)/(√(n) ) , x^(-) + Z_{(\alpha )/(2) }(S.D)/(√(n) ) )`

`(350 - 1.96(100)/(√(64) ) , 350 + 1.96(100)/(√(64) ) )`

`(350 -24.5, 350 +24.5)`

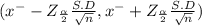
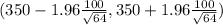
(325.5 ,374.5)

b)

Explanation:-

Given mean of the Population μ = 400

Given sample size n = 64

Given mean of the sample x⁻ = 350

Standard deviation of the Population σ = 100 hours

Null hypothesis : H₀:The manufacturer has right to take the average life of the light bulbs is 400 hours.

μ = 400

Alternative Hypothesis: H₁: μ ≠400

The test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (350 -400)/((100)/(√(64) ) )`

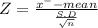
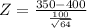
|Z| = |-4|

The tabulated value Z₀.₉₅ = 1.96

The calculated value Z = 4 > 1.96 at 0.05 level of significance

Null hypothesis is rejected.

Conclusion:-

The manufacturer has not right to take the average life of the light bulbs is 400 hours.