Answer:
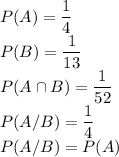
A and B are not independent events.
Explanation:
Total number of possibilities is 52 (Total number of cards in the deck).
Formula for probability of an event E can be observed as:
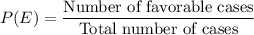
For event A, number of cases possible for a card to be diamond = 13
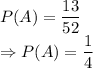
For event B, number of cases possible for a card to be a king = 4
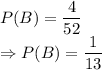
For the event,
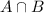 , the card is a king and diamond, only one case is possible.
, the card is a king and diamond, only one case is possible.
Because there is only one card for king of diamond.
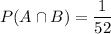
Formula for P(A/B):
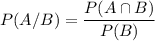
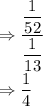
Yes, P(A) is same as P(A/B).
Here, A and B are not independent events because they have a common case i.e. a king is there which is of diamond in the deck.