Question

The overhead reach distances of adult females are normally distributed with a mean of 197.5 cm197.5 cm and a standard deviation of 8.3 cm8.3 cm. a. Find the probability that an individual distance is greater than 210.90210.90 cm. b. Find the probability that the mean for 1515 randomly selected distances is greater than 196.00 cm.196.00 cm. c. Why can the normal distribution be used in part​ (b), even though the sample size does not exceed​ 30?

Answer 1

a) 5.37% probability that an individual distance is greater than 210.9 cm

b) 75.80% probability that the mean for 15 randomly selected distances is greater than 196.00 cm.

c) Because the underlying distribution is normal. We only have to verify the sample size if the underlying population is not normal.

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

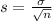For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this question, we have that:

`\mu = 197.5, \sigma = 8.3`

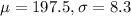
a. Find the probability that an individual distance is greater than 210.9 cm

This is 1 subtracted by the pvalue of Z when X = 210.9. So

`Z = (X - \mu)/(\sigma)`

`Z = (210.9 - 197.5)/(8.3)`

`Z = 1.61`

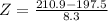
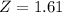
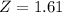`Z = 1.61` has a pvalue of 0.9463.

1 - 0.9463 = 0.0537

5.37% probability that an individual distance is greater than 210.9 cm.

b. Find the probability that the mean for 15 randomly selected distances is greater than 196.00 cm.

Now
`n = 15, s = (8.3)/(√(15)) = 2.14`

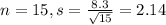
This probability is 1 subtracted by the pvalue of Z when X = 196. Then

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (196 - 197.5)/(2.14)`

`Z = -0.7`

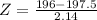
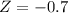
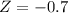`Z = -0.7` has a pvalue of 0.2420.

1 - 0.2420 = 0.7580

75.80% probability that the mean for 15 randomly selected distances is greater than 196.00 cm.

c. Why can the normal distribution be used in part​ (b), even though the sample size does not exceed​ 30?

The underlying distribution(overhead reach distances of adult females) is normal, which means that the sample size requirement(being at least 30) does not apply.