Question

An archer draws her bow and stores 34.8 J of elastic potential energy in the bow. She releases the 63 g arrow, giving it an initial speed of 28 m/s. How efficient is the transfer of the elastic potential energy of the bow to the kinetic energy of the arrow?

Answer 1

Approximately
`71\%`.

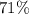Step-by-step explanation:

The formula for the kinetic energy
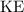`\rm KE` of an object is:

`\displaystyle \mathrm{KE} = (1)/(2)\, m \cdot v^2`,

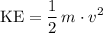where

• 
  `m` is the mass of that object, and
• 
  `v` is the speed of that object.

Important: Joule (
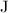`\rm J`) is the standard unit for energy. The formula for
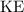`\rm KE` requires two inputs: mass and speed. The standard unit of mass is
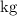`\rm kg` while the standard unit for speed is
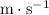`\rm m \cdot s^(-1)`. If both inputs are in standard units, then the output (kinetic energy) will also be in the standard unit (that is: joules,

Convert the unit of the arrow's mass to standard unit:

`m = 63\; \rm g = 0.063\; \rm kg`.

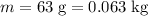Initial
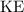`\rm KE` of this arrow:

`\begin{aligned}\mathrm{KE} &= (1)/(2) \, m \cdot v^2 \\ &= (1)/(2)* 0.063\; \rm kg * \left(\rm 28 \; m \cdot s^(-1)\right)^2 \\ &\approx 24.696\; \rm J\end{aligned}`.

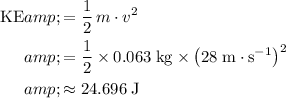That's the same as the energy output of this bow. Hence, the efficiency of energy transfer will be:

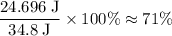`\displaystyle (24.696\; \rm J)/(34.8\; \rm J) * 100\% \approx 71\%`.