Answer:
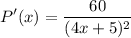
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/bz16ipe6p14y3f6abzxt2zy0j41tg530u9.png)
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2021/formulas/mathematics/college/kqosumt4896r7x44jgtw0o7kk6g4d3irvr.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2021/formulas/mathematics/college/526v84fft3iovys57h8fyaznapbe78t2md.png)
Explanation:
Step 1: Define
Identify
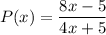
Step 2: Differentiate
- Derivative Rule [Quotient Rule]:
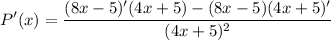
- Basic Power Rule [Derivative Properties]:
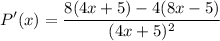
- Expand:
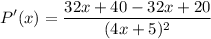
- Simplify:
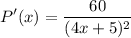
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation