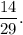Question

A company is producing two types of ski goggles. Thirty percent of the production is of type A, and the rest is of type B. Five percent of all type A goggles are returned within 10 days after the sale, whereas only two percent of type B are returned. If a pair of goggles is returned within the first 10 days after the sale, the probability that the goggles returned are of type B is

Answer 1

`(14)/(29)`

Explanation:

Let P(A) be the probability that goggle of type A is manufactured

P(B) be the probability that goggle of type B is manufactured

P(E) be the probability that a goggle is returned within 10 days of its purchase.

According to the question,

P(A) = 30%

P(B) = 70%

P(E/A) is the probability that a goggle is returned within 10 days of its purchase given that it was of type A.

P(E/B) is the probability that a goggle is returned within 10 days of its purchase given that it was of type B.

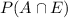`P(A \cap E)` will be the probability that a goggle is of type A and is returned within 10 days of its purchase.

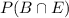`P(B \cap E)` will be the probability that a goggle is of type B and is returned within 10 days of its purchase.

`P(E \cap A) = P(A) * P(E/A)`

`P(E \cap A) = (30)/(100) * (5)/(100)\\\Rightarrow P(E \cap A) = 1.5 \%`

`P(E \cap B) = P(B) * P(E/B)`

`P(E \cap B) = (70)/(100) * (2)/(100)\\\Rightarrow P(E \cap B) = 1.4 \%`

`P(E) = 1.5 \% + 1.4 \% \\P(E) = 2.9\%`

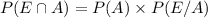
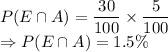
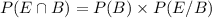
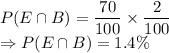
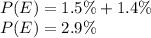
If a goggle is returned within 10 days of its purchase, probability that it was of type B:

`P(B/E) = (P(E \cap B))/(P(E))`

`\Rightarrow (1.4 \%)/(2.9\%)\\\Rightarrow (14)/(29)`

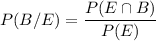
So, the required probability is
`(14)/(29).`