Answer: 167
Step-by-step explanation: To find the 76th term of this arithmetic sequence, we will be using our explicit formula which is shown below.

Since we want to determine the 76th term, we are going
to substitute 76 in for n in our explicit formula.
Then,
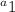 will be our first term in our sequence which is 17.
will be our first term in our sequence which is 17.
Lastly, d is our common difference or the difference between each of the terms in our arithmetic sequence which is 2.
So we have
 .
.
Now we have all the information we need. Just simplify from here.
Make sure to apply order of operations because this is where many
students make mistakes. Inside the parentheses first!
(76 - 1) is going to be 75.
So we have
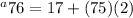 .
.
Then, we have to make sure we multiply before we add.
So (75)(2) is going to give us 150.
So we have
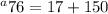 .
.
Now just add to find that
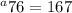 .
.
So the 76th term is 167.