The teacher decides that no student can win twice, so she removes the tickets of the first winner before drawing the second winner.
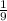 is the probability that she draws Kitzen first and then Ava second.
is the probability that she draws Kitzen first and then Ava second.
When the teacher removes Kitzen's ticket before drawing the second winner, the total number of tickets is reduced by 12. The updated number of tickets for the remaining students is as follows:
Ava: 16 tickets
Sam: 11 tickets
Josie: 9 tickets
The total number of remaining tickets is 16+11+9=36.
Now, to find the probability of drawing Kitzen first and then Ava second, you multiply the probabilities of each event.
Probability of drawing Kitzen first:
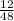 (since there are initially 48 total tickets)
(since there are initially 48 total tickets)
Probability of drawing Ava second:
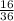 (after Kitzen's ticket is removed)
(after Kitzen's ticket is removed)
Now, multiply these probabilities:
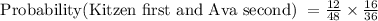
Simplify the fraction:
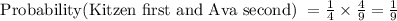
So, the probability that the teacher draws Kitzen first and then Ava second is
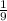 .
.