Answer:
center =
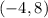
Radius = 7 units
Explanation:
Given: Equation of circle is
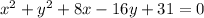
To find: Radius and center of the circle
Solution:
Equation of circle is
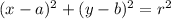
Here,
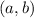 is the center and r is the radius.
is the center and r is the radius.
![x^2+y^2+8x-16y+31=0\\\left [ x^2+2(4)x+4^2 \right ]+\left [ y^2-2(8)y+8^2 \right ]+31=4^2+8^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/2qbuizto99f0uikppm7oj58j74e26c7fl2.png)
Use formula
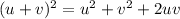
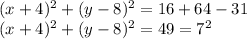
On comparing this equation with equation of circle,
center =
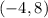
Radius = 7 units