Answer:
A sample size of 657 is needed.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
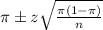
In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
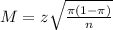
95% confidence level
So
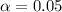 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
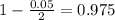 , so
, so
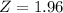 .
.
In the past, 19% of all homes with a stay-at-home parent had the father as the stay-at-home parent.
This means that
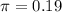
(a) What sample size is needed if the research firm's goal is to estimate the current proportion of homes with a stay-at-home parent in which the father is the stay-at-home parent with a margin of error of 0.03?
A sample size of n is needed.
n is found when
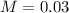
Then
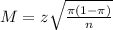
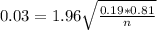
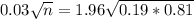
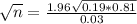
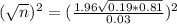
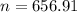
Rounding up to the nearest whole number.
A sample size of 657 is needed.