Answer:
The total cost of painting the deck and add fencing is $1,386.79.
Explanation:
Consider the diagram below.
The smaller circle represents Jeanine’s swimming pool with diameter,
d = 27 feet.
And the outer circle represents the deck.
The width of the deck is 5 feet.
Then the diameter of the bigger circle is:
D = 27 + 5 + 5 = 37 feet
It is provided that Jeanine wants to paint the deck and the paint costs $0.85 per square foot.
The cost of painting the deck can be computed using the formula:
Cost of painting = Area of Deck × Cost of paint/square foot
Compute the area of the deck as follows:
Area of Deck = Area of bigger circle - Area of smaller circle
![=\pi R^(2)-\pi r^(2)\\\\=\pi(R^(2)-r^(2))\\\\=(22)/(7)* [((37)/(2))^(2)-((27)/(2))^(2)]\\\\=502.86](https://img.qammunity.org/2021/formulas/mathematics/college/86ylyqea18ww1o9nuqtek1doomau854zlo.png)
Then the cost of painting the deck is:
Cost of painting = Area of Deck × Cost of paint/square foot
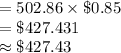
The cost of painting the deck is $427.43.
Now Jeanine also wants to put a fence around the deck.
The cost of fencing is, $8.25 per foot.
The cost of putting the fence can be computed using the formula:
Cost of putting the fence = Circumference of the big circle × Cost of fencing
Compute the cost of putting the fence as follows:
Cost of putting the fence = Circumference of the big circle × Cost of fencing
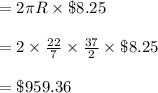
The cost of putting the fence is $959.36.
The total cost of painting the deck and add fencing is:
Total Cost = Cost of painting the deck + Cost of putting the fence
= $427.43 + $959.36
= 1386.79
Thus, the total cost of painting the deck and add fencing is $1,386.79.