Question

To test if the mean IQ of employees in an organization is greater than 100, a sample of 30 employees is taken and the value of the test statistic is computed as t=1.42. If we choose a right tailed test at a 5% significance level, we

a) do not reject the null hypothesis and conclude that the mean IQ is not greater than 100
b) do not reject the null hypothesis and conclude that the mean IQ is greater than 100
c) reject the null hypothesis and conclude that the mean IQ is not greater than 100
d) reject the null hypothesis and conclude that the mean IQ is greater than 100

Answer 1

`p_v =P(t_((29))>1.42)=0.0831`

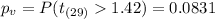
For this case the p value calculated is higher than the significance level used of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case would be:

a) do not reject the null hypothesis and conclude that the mean IQ is not greater than 100

Explanation:

Information given

We want to verify if he mean IQ of employees in an organization is greater than 100 , the system of hypothesis would be:

Null hypothesis:
`\mu \leq 100`

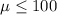
Alternative hypothesis:
`\mu > 100`

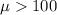
The statistic for this case is given by:

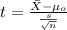`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

The statistic calculated for this case
`t_(calc)= 1.42`

The degrees of freedom are given by:

`df=n-1=30-1=29`

Now we can find the p value using tha laternative hypothesis and we got:

`p_v =P(t_((29))>1.42)=0.0831`

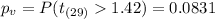
For this case the p value calculated is higher than the significance level used of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case would be:

a) do not reject the null hypothesis and conclude that the mean IQ is not greater than 100