Answer:
The z score of the 65-mph speed limit is -0.75
Explanation:
The z score is given by the relation;
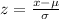
Where:
Z = Normal (Standard) or z score
x = Observed speed score
μ = Mean, expected speed
σ = Standard deviation
Where we plug in the values for x = 65-mph, σ = 8 mph and μ = 71 mph, into the z-score equation, we get;
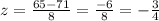
Hence the z score of the 65-mph speed limit =-3/4 or -0.75.